Тестовый раздел
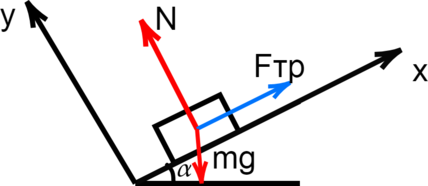
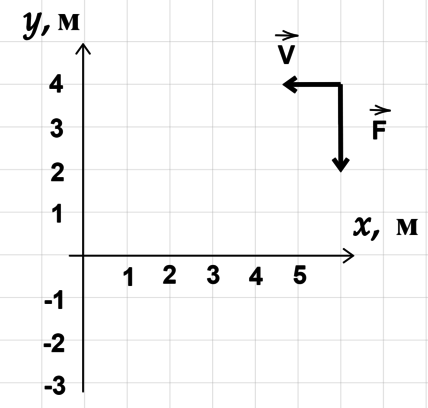
Кот Тимофей толкает брусок массой \(m=15\, \text{кг}\), равномерно движущийся по льду, с силой \(F=12\,H\) в направлении движения. Каково ускорение бруска в инерциальной системе отсчета, связанной со льдом?
Воспользуемся вторым законом Ньютона: \[\vec{F} = m\vec{a} ,\] из которого: \[a=\frac{F}{m} = \frac {12}{15}= 0{,}8 \, \text{м/с}^2\]
Ответ: 0,8
На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей приложенных к телу сил.
Построим вектор \(F1'\), который выходит из точки \(B\), параллельно вектору \(F1\)
Соединим точку \(A\) с концом вектора \(F1'\). Получим искомый вектор \(F\)
Ответ: 3
Брусок покоится на наклонной плоскости, образующей угол \(a\)=\(30^{\circ}\), его масса \(m\)=0,1кг. Найдите силу трения покоя, которая действует на брусок
Отметим все силы, действующие на брусок, а также введем координатную плоскость. Ось \(x\) направим вдоль наклонной плоскости, а ось \(y\) перпендикулряно ей.
Запишем 2 закон Ньютона: \[F=m a\] где \(F\) – сумма всех сил, действующих на тело, \(a\) – его ускорение, \(m\) – масса тела
Так как брусок покоится, то его ускорение равно 0. Запишем 2 закон Ньютона на ось \(x\): \[F_{\text{тр}} -mg \sin a=0\]
Выразим \(F_{\text{тр}}\): \[F_{\text{тр}}=mg \sin a\]
Подставим числа из условия: \[F_{\text{тр}}=0,1 \text{ кг} \cdot 10 \text{ Н/кг} \cdot \frac{1}{2}=0,5\text{ Н}\]
Ответ: 0,5
В инерциальной системе отсчета сила \(F\) сообщает телу массой \(m\) ускорение 9 м/c\(^2\).
Какое ускорение сообщает сила 1/3 F в этой же системе отсчета телу массой \(3m\)
В инерциальной системе отсчета тело движется по 2 закону Ньютона: \[F=m \cdot a\] где \(m\) масса тела, а \(a\) - его ускорение
Для первого случая: \[F=9m\] выразим \(m\): \[m=\frac{F}{9} \quad (1)\]
Запишем 2 закон Ньютона для второго случая: \[\frac{1}{3} F = 3m \cdot a_{2}\] выразим \(a_{2}\): \[a_{2} = \frac{F}{9m} \quad (2)\]
Подставим (1) в (2), получим: \[a_{2}=\frac{F}{9F}=1\]
Ответ: 1
В инерциальной системе отсчета сила \(\Vec{F}\) сообщает телу массой \(m\) равное по модулю 4 м/с\(^2\). Во сколько раз масса второго тела меньше массы первого, если ускорение второго тела \(a_{2}\)=16 м/c\(^2\) под действием силы \(2\Vec{F}\) в этой системе отсчета
В инерциальной системе отсчета тело движется по 2 закону Ньютона: \[F=m \cdot a\] где \(m\) масса тела, а \(a\) - его ускорение
Для первого случая: \[{F}=4m_{1} \quad (1)\]
Для второго случая: \[{2F}=16m_{2} \quad (2)\]
Подставим (1) в (2), получим: \[8m_{1}=16m_{2}\]
\[m_{1}=2m_{2}\]
Следовательно масса второго тела в 2 раза меньше массы первого тела
Ответ: 2
В инерциальной системе отсчета сила \({\vec F}\) сообщает телу массой \(m\) ускорение \({\vec a}\). Модуль ускорения равен \(a=2\, \text{м/с}^2\). Определите модуль ускорения, которое сообщается телу массой \(4m\) модулем силы \(5F\) в этой системе отсчета.
Воспользуемся вторым законом Ньютона для двух случаев: \[{\vec F}=m{\vec a}\] \[5{\vec F}=4m{\vec a_1},\] где \(a_1\) - искомое ускорение Для нахождения \(a_1\) поделим уравнения: \[\frac{F}{5F}=\frac{ma}{4ma_1}\] \[a_1=\frac{5a}4=\frac{5\cdot 2}4=2,5 \text{ м/с}^2\]
Ответ: 2,5
Мяч массой \(m=2 \,\text{кг}\) свободно катится по гладкому горизонтальному столу параллельно оси \(Ox\) со скоростью \(\upsilon = 5\,\text{м/с} \). В момент времени \(t=0\,\text{с}\), когда мяч находился в точке \(A\), на него начинает действовать сила \(\vec{F}\), модуль которой равен \(F=0{,}5\,H\). Чему равна координата мяча по оси \(Oy\) в момент времени \(t=5\,\text{с}\)?
Так как на тело действует сила, значит появляется ускорение, сонаправленное с действующей силой. Из 2 закона Ньютона вычислим ускорение: \[F=ma\] \[a=\frac{F}{m}=\frac{0{,}5}{2}=0{,}25\,\text{м/с}^2\] Заметим, что сила противоположна направлению оси \(Oy\), тогда проекция ускорения будет с отрицательным знаком. Также отметим, что \(\upsilon_{y0}=0 \,\text{м/с}\).
Координата мяча по оси \(Oy\) вычисляется по формуле: \[y=y_0 + \upsilon_{y0} t + \frac{a_y t^2}{2}= 4+ 0\cdot 5 + \frac{-0{,}25 \cdot 5^2}{2}= 0{,}875\,\text{м}\]
Ответ: 0,875
